液体经快速冷却转变为无序非晶态的过程叫做玻璃转变。为什么在很窄的温度区间，体系的粘度可以增加十几个量级从流动液体变为刚性固体，但是原子排布却没有明显变化？关于此难题，诺贝尔物理学奖获得者安德森指出：“玻璃转变是凝聚态物理中未解决的最难、也最有意义的问题之一。”《Science》期刊也将其列为125个科学问题之一。

通过构建一种结构参数，可以有效区分玻璃态和液体，并将其与过冷液体的动力学减缓(dynamical slowing down)联系起来，是玻璃转变研究领域长期存在的挑战之一。目前已经提出了两类结构量来表征动力学减缓：1）结构不可知(structural agnostic)参量，如结构熵、相关长度、和机器学习特征等；2）局部偏好结构（即几何意义明确）参量，如二十面体、四面体和类晶体团簇等，这些结构依赖于系统，也不能同时适用于二维和三维。此外，这些参数在玻璃转变处没有明显变化，也就是说，它们无法区分玻璃态和液体。

为克服上述限制，西安交大美高梅mgm1888公司官网张会军副教授、刘峰教授与香港科大章琪博士、韩一龙教授合作，基于局部笼结构的Voronoi构造，提出各向异性结构参量k = R_min/R_max (R_min和R_max分别代表Voronoi单元的短轴和长轴)，具有明确的几何含义，在模耦合理论(mode-coupling theory)推测的玻璃转变处表现出明显的变化(图1)，揭示了玻璃转变是从局部结构不均匀形变的液体到均匀形变的固体变化的过程，这在二维和三维系统中具有鲁棒性（如下图）。相关论文以《笼结构各向异性-各向同性转变揭示玻璃转变的结构特征》(Anisotropic-Isotropic Transition of Cages at the Glass Transition)为题发表于Phys. Rev. Lett.期刊。

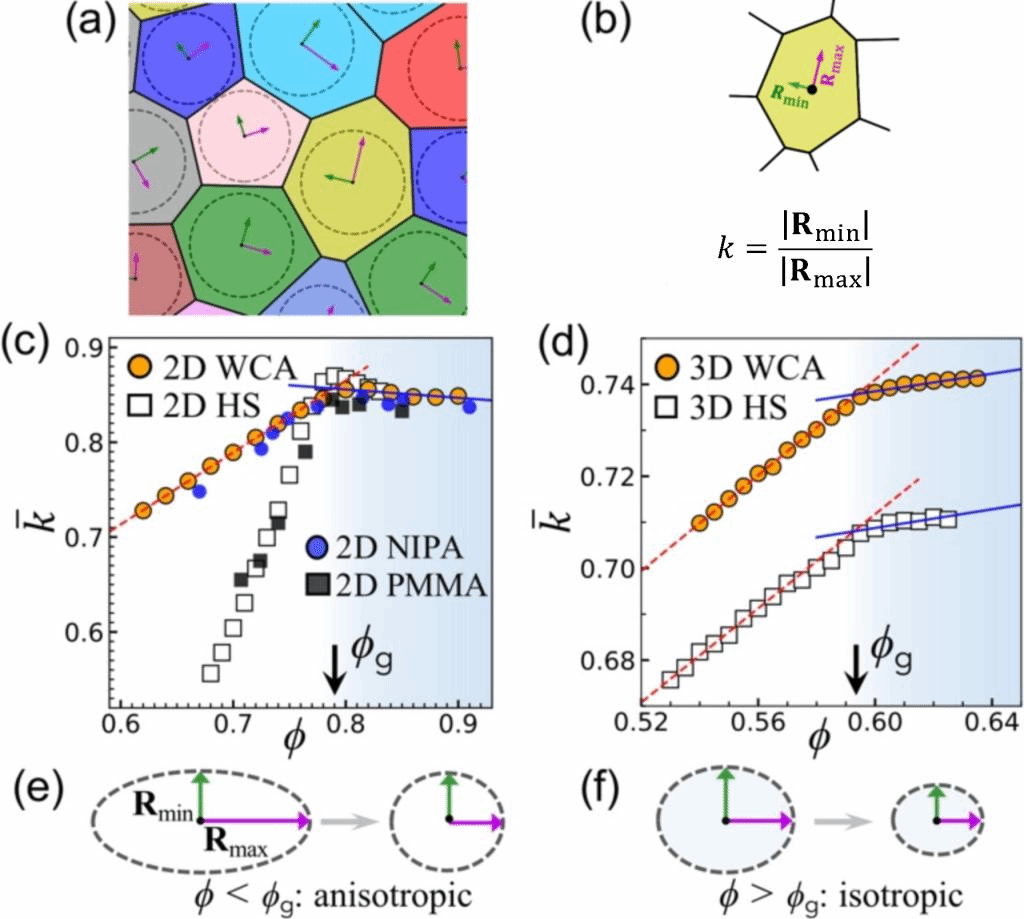
图1. 基于Voronoi构造的各项异性参量k揭示玻璃转变。

作者进一步展示了k的两个应用：(1) 解释结构幂律v_a ∝ q₁^−d (v_a为平均体积，q₁为结构因子第一峰位)在液体区 d > D (空间维度)和在玻璃区d = D的现象，这为区分液体和玻璃态提供另一个结构特征 (图2)。这种幂律仅在玻璃态中被研究。这里，作者将此幂律推广到过冷液体也是一个重要的发现。(2) 通过将k代入经典的自由体积模型来预测扩散常数，可将动力学与单粒子尺度结构联系起来(图3)。

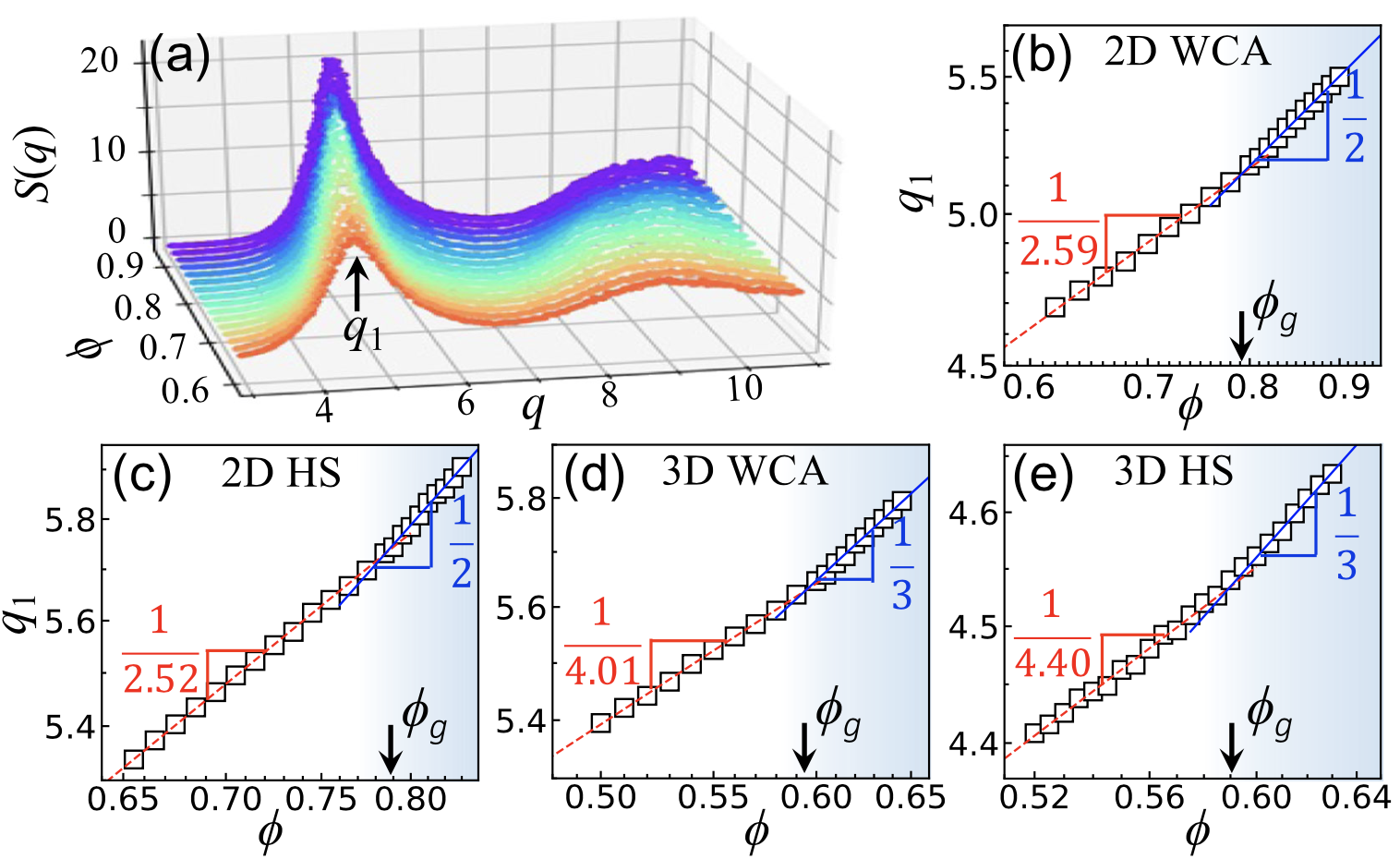
图2. 结构因子幂律v_a ∝ q₁^−d揭示玻璃转变过程从液体d > D 到玻璃态d = D.

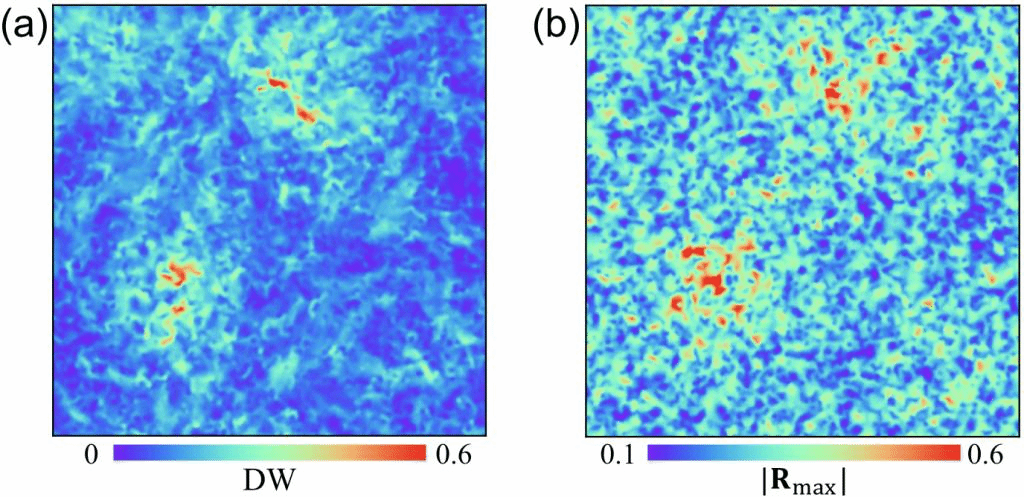
图3. 过冷液体动力学与各项异性参数k中长轴相关联。

【论文】Huijun Zhang^*, Qi Zhang, Feng Liu, and Yilong Han^*, Anisotropic–Isotropic Transition of Cages at the Glass Transition. Phys. Rev. Lett. 132, 078201 (2024).

DOI: https://doi.org/10.1103/PhysRevLett.132.078201

【软物质模拟课题组主页】https://gr.xjtu.edu.cn/zh/web/huijun

张会军副教授从事软物质物理的理论与模拟研究，工作以第一作者发表于Physical Review X, Physical Review Letters, Nature Communications, Acta Materialia, Communications Physics,  Physical Review E等著名期刊。

【招生】课题组招收具有材料、物理、力学，机械、化学等相关专业的硕士、博士研究生和研究助理，研究条件优越，欢迎加入！

联系邮箱：huijun@xjtu.edu.cn。